液压成形轴对称壳体的金属薄板力学研究
液压成形轴对称壳体的金属薄板力学研究
膜应力在轴对称壳的分析使用一个新定义的几何量称为流动度-一个不同于曲率的量膜应力迄今为止一直相关。
by T. C. Hsu and H. M. Shang
摘要—新方法的推导过程称为膨胀试验,从薄膜应力公式,几何和压力之间的关系在一个薄壳内部压力。摘要介绍了一种称为“适当性”的量纲来消除局部几何与完美球面的关系,并证明了“适当性”是一种不同于曲率的几何性质。对恒渗表面的形状和这种形状薄壳的应力进行了检查。介绍了本工程中使用的特殊实验技术,并给出了实验结果。人们发现,形成的金属壳只有在极点和沿一个恒定纬度的圆是完美的球形。在这个圆里面,贝壳是长的(或者比球体更尖),而在它外面,它是扁圆的(或者比球体更平)。随着成形过程的进行,这一完美球面的圆会不断扩大,直至成形过程变得不稳定,整个球面变长。并讨论了成形过程中各阶段的应力分布。
介绍
在本项目中研究的成形过程包括将金属薄板夹紧在带有圆孔的模具上,并使金属薄板的一侧承受不断增加的液压压力。这样,钣金工件就被推入模具的孔中,形成一个近似扇形的壳体。在标准条件下,这一过程被广泛用于测试金属板的成形性,称为“凸点试验”,然后将无断裂凸点的最大极高度作为成形性的指标.
这一著名的过程是过去二十年来许多研究论文的主题1'5,该过程的基本平衡和相容方程是众所周知的。然而,控制这一形成过程的基本方程并不能得到显式解;换句话说,用数学术语来说,这个问题本质上是不确定的。迄今为止,这些方程的预测解是通过引入对凸起形状、材料中的应力-应变关系或材料颗粒路径的各种假设来获得的。这些解在不同程度上与实验结果一致,从而在不同程度上证明了所作的假设。然而,他们并没有帮助探索实验结果本身的详细含义;事实上,这些解决办法并不是为了这个目的而寻求的。本文没有尝试预测理论;通过对一些精确的实验结果的研究,得出了一些结论,这些结论不仅适用于金属壳体,也适用于其他穹顶、壳体、灯泡和气球。本文对这种方法的合理性和成果进行了阐述。.
曲率与膜应力的关系
在轴对称壳体中,主应力的方向在环向和子午切向是对称的。如σ为膜应力,p为弯曲半径,p为水力压力,t为局部厚度,下标e和s分别为周向和经向切向,则膜应力方程为,
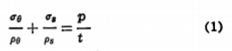
该方程是一个简单的平衡方程,可通过考虑壳体中边沿主曲率方向的小矩形单元的平衡来推导。在图1,其中展示了子午线和计划的隆起部分,作为as 和 ps的平面纸pe在一架飞机通过PQ和垂直于纸上。两个半径曲率、pe 和pSl如图1中的PQ和PS所示。从几何上看,pe是局部次法线,等于r/sin e。考虑到工件在纬度P以上的平衡,得到:

从对eq(1)和(2)的仔细检查中,我们可以推导出一些关于为获得理论解而作出的假设的结论。实际形成的壳的形状近似于一个球体,可能由于这个原因,过去的一些预测理论假定球形,而解释理论则使用等效球体。然而,壳的形状在表面上可能与球相似,然而,实际的曲率可能与球壳有很大的偏差,因为曲率依赖于坐标的二阶导数。因此,在方程式(1)和(2)中可以很容易地看出,假设壳体为球形将导致不准确的理论结果,至少就应力而言是如此。
由于应力直接与曲线有关,因此对曲线尾部的曲率进行分析并以适当的精度进行测量是可取的。在分析曲率时,可以方便地利用等均匀曲率的球面作为范数,并考虑与完美球面形状的偏差。因此,结合eq(1)(2)可得:

方程(3)表示了应力比(变形方式所依赖的应力比)与主曲线比(代表局部变形的一个方面)之间的一个非常简单的关系
压力容器中应力与流动度的关系
主曲率的比值pe/ps具有基本的几何意义,因为它提供了偏离球面形状的定量测量。称它为n值比较方便。因此,当N为0时,eq(3)适用于环向应力为纵向应力两倍的圆柱体或圆锥,当N为1时,适用于应力条件为平衡拉伸的球体。n值2是特别重要的,因为在这样的曲率表面,周向应力消失。探索等n曲面的形状和其中的应力是很有趣的。
在图2所示的四分之一子午线交会¬规划设计的各种constant-N表面,绘制按照参数方程推导在附录a .完整的表面可以可视化想象下面的曲线在图2镜像轴,旋转所产生的表面对R-axis这些曲线。从图2中可以看出,当2v值为0或
相反,恒lv表面是柱状的,顶部和底部是开放的。当N值从0增加到1时,表面的形状从圆柱形变成又长又尖的形状,再变成更短的香肠和橄榄,当N等于1时达到球体。当N值为2时,表面的形状就像橘子,随着N的不断增大,表面就变得像更平更薄的煎饼的表面。
在N的正值范围内,将(1 -N)定义为长毛是有用的,因为这个数字越大,常数N曲面延长得越长。长毛的反面当然是扁性。因此,一个有界的圆平面是一个无限扁率的表面,而一个圆柱或圆锥是曲率之一。曲面的曲率是两个主曲率的平均值,而曲率与主曲率的比值有关。这一区别将在本文后面用实验结果加以说明。
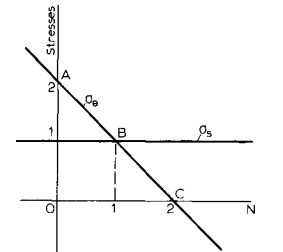
图3主应力比值随n值变化
图四—曲面曲率半径随径向坐标的变化
值得注意的是延伸性和弯曲性是两个截然不同的几何特性。一个表面可以是长而小的曲率,也可以是长而大的曲率。曲面的曲率是两个主曲率的平均值,而曲率与主曲率的比值有关。这一区别将在本文后面用实验结果加以说明。
任意轴对称壳体的应力比与N值的关系如图3所示,其中以子午切向应力(σs)为单位。在图2中,当N = 2时,点A代表圆柱(或圆锥),点B代表球面,点C代表橘形表面。这三点将应力划分为四个范围。在C点(N > 2)的右边,环向应力是压扁的,其形状比“橘子”更扁圆。在点B和点C之间,(拉伸)周向应力小于扁壳的子午切向应力,且在A点和B点之间,在长椭球壳中,周向应力大于经向切向应力。在点A的左边,N是负的,表面不再封闭,并且,如果一个容器是由适合的末端和这样的护柱形的边制成,箍应力将是纵向应力的两倍以上。
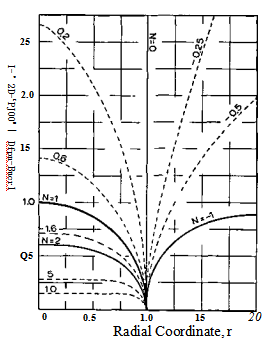
对等N曲面壳体的应力(而不是应力比)的检验将表明,严格地说,只有延长表面是可行的。图4显示了pe随半径r的变化,取赤道半径为1,如图2所示。由式(2)可以看出,图4中的pe也代表了等厚度壳体的子午应力。因此,对于所有N大于一的等N面,应力(rs在极点理论上是有限大的。在实践中,这种应力的理论方向从未实现,因为,一方面,存在弯曲应力,壳体被弹性地塑造成有限曲率的局部形状,另一方面,应力集中可以通过在韧性材料中进行局部屈服来缓解。当然,我们没有理由不把有用的压力容器做成n值恒定大于1的形状,但要适当地调整其两极的形状。另一方面,在等N曲面中;在两极的材料总是无应力的。将图4与图3结合起来,可以推测出周向应力的变化
实验方法
压力容器的优点是表面具有恒定的n值,特别是当它们被制造成材料在一个方向上比在另一个方向上弱时。因此,在灯泡、圆屋顶、贝壳和气球的设计中,形状与恒定表面应力之间的关系对于承受内外压力具有重要意义。然而,在本项目的背景下,不建议拟合实验壳与恒定w曲面进行分析。本文还讨论了恒流面及其应力,以说明恒流面应力的意义,并对探索实验壳中恒流面应力的变化具有重要意义。
本文的实验结果是用加压油将薄铜片制成直径约0.152米、最大极高5.21厘米的壳。在本节中,对测量和计算方法进行了描述,因为它们是特殊的方法,没有它们就不可能进行本文所述类型的研究。
本项目最重要的技术是用车间量角器代替纵向坐标,精确测量壳体子午斜率6(图1)。通过这样做,得到经向斜率所必需的图解或数值微分 dl/dr (见 Fig. 1) 绕过。用移动显微镜测量径向坐标r。径向坐标r然后被绘制成 和sinΦ的曲线, 曲率半径 pe被确定。.
为确定壳体内各点的N值,采用子午截面曲率半径pS。因此,根据定义,
方程(6)的微分用图形表示。.
结果和讨论
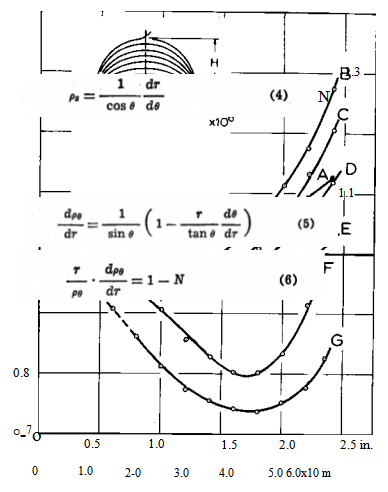
壳牌的n值的变化变化¬诸多阶段的形成过程是如图5所示,形成从曲线,曲线G(钢管的材料断裂曲线G)。图5中的七个曲线可以分成三组:在曲线。第一组,代表过程的初始阶段;第二组中的曲线B到D,用于稳定条件下的主要过程;当温度不稳定时(油压保持常值时),曲线从E到G。
我们可以看到在图5中,直到这个过程变得不稳定,外壳是完美的球形(N = 1),只有在北极(r = 0),以及一个圆(由曲线和直线的交点N = 1)。在这个圆,表面扩展的(N =1),或比一个球体更指出,和外面扁,或者比球体更扁平。在薄板材料成形的过程中,表面完全为球形的圆不断膨胀,直到不稳定变形的后期,整个壳体变长。
曲线A和曲线B之间的区别说明了曲率和曲率之间的区别。由于显而易见的原因,随着极高度的增加,壳体的一般曲率也会增大。因此,从曲线A到曲线B,壳体的曲率变大。然而,在图5中,我们可以看到,在靠近边缘的区域,斜度从A减小(或N增加)到b。因此,完全符合逻辑的说法是,一个表面变成了一个更大的曲率,但同时变得更平坦;这正是曲线A和B之间的情况。
对于铝板的结果(这里没有给出)显示了径向坐标r的相同的一般变化,即从极点到边缘,n值在统一以下下降,然后增加到一个大于统一的值。
为了说明壳体形状对壳体内应力的影响,将壳体内应力以无因次形式表示。为此,将eq(2)(3)改写为:
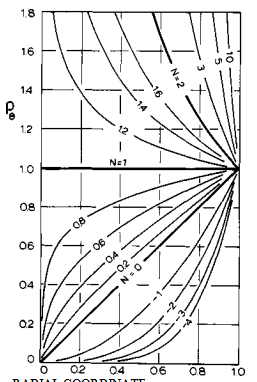
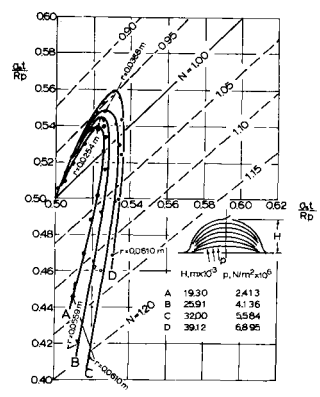
其中R为极点处的曲率半径。因此eq(7)和eq(8)的左手边分别是无因次的子午切向应力和周向应力。用这种形式表示,厚度、压力和一般曲率的影响被消除,而仅仅揭示了延迟性对应力的影响。eq(7)和(8)中的两个无量纲应力在图6(a)和6(b)中相互对应。在这两幅图中,应力状态由从原点(0,0)到曲线上一点的矢量表示。如果壳体是极曲率的完美球面,矢量的末端在点(%,%);而从点(%,%)开始的曲线的长度是对由于实际壳体内的流变性引起的应力大小和应力比值变化的量度。
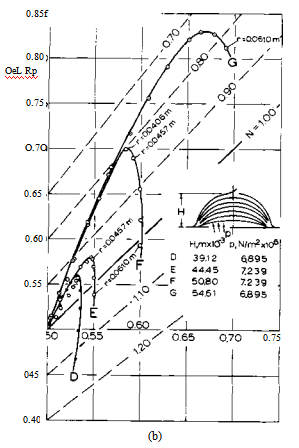
在图6(a)和图6(b)中,在N = 1的线上方,周向应力大于平面切向应力;在这条线下面,情况正好相反。因此,在靠近磁极的区域,材料沿圆周方向的拉伸比沿切线方向的要大。这种变形会产生一个更长的(尖的)形状,这与通常的想象相反,尽管它可以通过参考图被认为是真实的。
在图6(b)中,从图6(a)重复曲线D,以显示图6(a)与6(b)的相对比例。从图6(b)中可以看出,随着非稳定变形的增大,两种应力覆盖更大的范围;换句话说,应力变得不均匀。对比图6(a)和图6(b)也可以看出,稳定范围和不稳定范围之间的应力分布性质发生了剧烈变化。
结论
研究结果揭示了轴对称壳体胀形试验和膜应力的一些有趣的特征。从成形过程的理论研究来看,球形成形的假设是不充分的。所以工程应用而言,试验¬心理技术和本文提供的分析结果的方法是很有用的实际过程的调查,他们的改进更好的厚度分布,例如,通过改变拉紧(或法兰的内运动),或对凹模的表面形成,只有两种可能。
从设计师的角度来看,应力分布的控制通过形状打开新的可能性的prolateness增援的最佳位置,强调由于轻微变化的再分配在形状服务由于弹性或蠕变应变,对屈曲阻力设计,或适当的厚度分布在橡胶制品膨胀后实现正确的形状。
此外,还介绍了一种几何支柱的定量测量方法,即拉伸度,并将其简单地应用于薄壳的膜应力。
转载请注明精川材料检测地址:www.jctest.vip




