蜂窝结构力学超材料弹性及抗冲击性能
超材料 (Meta-material) 是一种利用现有材料,如高分子材料、玻璃、金属及合金等,通过加工一定形式的拓扑结构而形成的一种人工材料结构。它具有自然材料所不具备的各种特殊功能,如负泊松比、负有效质量密度、负有效模量等。因其具有特殊的波动传播带隙,在隔振、吸声降噪、隐身、光信息和电磁波等工程领域拥有巨大的应用前景。
在超材料中有一类材料具有受拉时其垂直方向有膨胀的力学特性,即这类超材料具有“负泊松 (Poisson) 比”,又称为具有“拉胀性”(Auxetic)。同时,具有手性 (Chirality) 的超材料是近年来受到国内外学者广泛关注的一类超材料,其手性是由Lord Kelvin 于1894年提出的具有镜像对称而又不能完全重合的结构特性。手性超材料的一个最显著特征就是具有波的传播带隙。
在力学承载和多功能设计与应用方面,目前国内外学者广泛关注一类兼有“负泊松比”和手性的超材料,这类超材料的典型代表是由具有周期性分布的圆环状(节点环)和弹性韧带切向连接形成的蜂窝型拓扑结构,可能是平面结构也可能是三维空间结构(如图1所示)。 图1 韧带型力学超材料平面及空间三维结构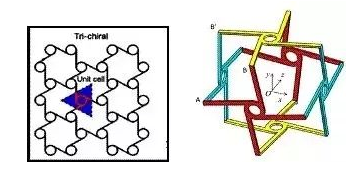
这类超材料因其拓扑结构可变、轻质及高比刚度,与普通多孔拓扑材料相比,该类材料具有更好的抗冲击能力、抗凹能力、能量吸收能力和减振隔噪的能力。特别地,在抗冲击的力学性能研究方面,通过对这种具有手性蜂窝结构的力学超材料进行有限元仿真和实验手段,可以观察冲击载荷对不同的手性蜂窝结构力学超材料的冲击形变特点,为优化此类材料的抗冲击性能设计提供理论基础。
1. 力学超材料弹性性能 1987年Lakes 首次通过聚氨酯泡沫获得具有特殊微观结构的负泊松比材料,并测得其泊松比值为-0.7。此后,新的具有“拉胀”(Auxetic) 特性的材料相继出现。1991年Lakes 等从微观的单元结构上总结了产生负泊松比应该具备的几个条件:旋转自由度、非放射性的动力学性能或者各向异性,并列举了普通蜂窝结构、内凹六边形蜂窝结构来论证自己的观点。此后,Lakes 等首次提出了六韧带手性蜂窝结构的力学超材料(非中心对称结构),这类材料可以使用金属母体材料制作,可以产生负泊松比并且可以大大提高工程承载能力。1997年Prall 等基于韧带变形模式对六韧带蜂窝结构力学超材料的负泊松比进行研究:对该种结构胞元产生负泊松比的力学机理首次进行了较为详细的描述(如图2所示)。
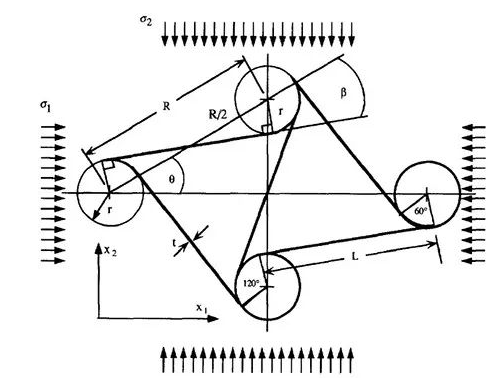
图2 六韧带胞元负泊松比形成的变形图
目前,国内针对手性蜂窝结构力学超材料的弹性性能的典型工作有:2013年赵显伟成功的推导出四韧带同向手性蜂窝结构的面内杨氏模量、泊松比、面外杨氏模量以及剪切模量的上限等,为今后手性蜂窝结构力学超材料的性能柔性化可变设计提供了理论依据。
2. 力学超材料抗冲击性能
一般工业领域特别是航空航天领域,对轻质、隔振、抗冲击等防护材料要求越来越高。针对手性蜂窝结构力学超材料,其抗冲击性能的研究的关键是确定外力和材料内部韧带及节点环上的作用力的大小。
2016年张新春等建立了六韧带手性蜂窝结构力学超材料的有限元模型,研究结果表明,随着冲击速度的增加,六韧带手性蜂窝结构表现为3种宏观变形模态:“><”型模式、“过渡”模式和“I”型模式,研究结果进一步反映了韧带和节点环在冲击吸能上的作用。
2017年卢子兴等对手性蜂窝结构力学超材料进行了面内冲击性能仿真实验,结果发现:各种不同类型手性系蜂窝结构力学超材料的变形模式较为一致。在低速冲击下,手性蜂窝的变形可分为两个阶段:第一个阶段为,联接韧带的弯曲卷绕和节点圆环的转动;第二阶段为,圆形环孔壁的坍塌。在高速冲击下,变形表现为圆形节点环和联接韧带的交替坍塌,胞元逐层压溃;而在中速冲击下,则表现为兼有低速和高速模式部分特征的过渡V 模式(如图3所示)。
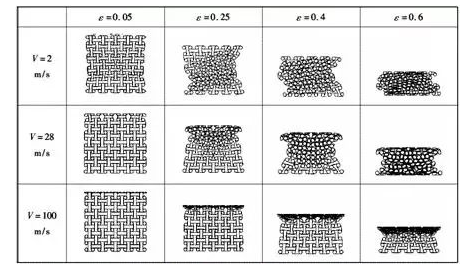
图3 不同冲击速度下四边反手性蜂窝材料变形模式
Spadoni 等将六韧带手性蜂窝结构力学超材料填充到大展弦机翼上(如图4所示),并进行了内部结构的设计、仿真和实验,结果证明了手性蜂窝结构填充材料可以承受大绕度的变形。总之,本文所讨论的手性蜂窝结构力学超材料在以上这些工程结构等领域中的应用研究,也进一步说明手性蜂窝结构力学超材料在工程实践中具有强大和广泛的应用潜力。对其性能与内部微结构关系的研究至关重要。
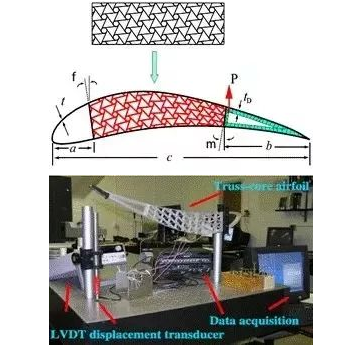
图4 六韧带填充机翼及实验装置
蜂窝结构力学超材料由于其独特的多参数微结构和优异的力学性能,且具有质轻、负泊松比、高剪切模量及良好的抗缺口、抗断裂以及高回弹韧性,受到了国内外研究人员的高度关注。由于其内部拓扑结构尺寸可以实现 mm-cm 量级的拓展,小到可用在生活和医用用品如血管支架、瓶塞、座垫上得到应用,大到可用于如航空、国防、汽车灯工业领域。近年来,关于手性蜂窝结构力学超材料的研究取得了许多积极成果,但大部分停留在实验制备与模拟仿真分析阶段。该领域尚存在很多值得探索的理论和实际应用问题。如内部受力、吸能机理以及进行力学超材料与其本身固有的电、波、声等性能的耦合分析、设计等。




