不同类型的材料存在不同的强度理论,常用的强度理论有四种。四种强度理论的相当应力最终由三个主应力按一定形式组合而成。针对具体的工程结构应力分析,首先需要根据材料类型选择合适的强度理论,进而关注所需的主应力组合形式。
工程机械结构材料以碳钢、合金钢等塑性材料为主,一般情况下采用第四强度理论进行设计。铸铁材料在一些非焊接结构上也有应用,这种情况的强度校核应该采用第一强度理论。
| 强度理论
| 应力及判据
| 适用材料
|
| 1 | 最大拉应力理论
| σ1≤σb
| 铸铁
|
2
| 最大伸长线应变理论
| σ1-μ(σ2+σ3)≤σb | 石料、混凝土
|
3
| 最大切应力理论
| σ1-σ3≤σs | 碳钢、铜、铝
|
4
| 畸变能密度理论
| Misses(σ1,σ2,σ3)≤σs | 碳钢、铜、铝 |
根据美国机械工程师协会(American Society of Mechanical Engineers,ASME)编著的《锅炉和高压容器规范》第三章第 1 部分 NB 段的描写,应力线性化是分析高压容器的一个重要部分。这里,我们需要将压力分为主要应力或次应力。主要应力用于保持力和力矩平衡的应力,次应力由其他效应引起。通常,次应力是由几何不连续性或位移控制的载荷引起的局部效应。次应力超过弹性极限时不会导致屈服破坏,因为它们已经重新分布了。在分析过程中,应力分析沿截面的多条线进行,称为应力分类线(stress classification lines,SCL)。由于 应力分类线 不唯一,因此我们必须根据工程判断来确定关键的线路。尽管不是完全正确(但是保守),线性化应力有时被视为等效于主要应力。如果无需详细说明,该规范的基本要求是:
- 主要膜应力的应力强度(Tresca 等效应力)不应超过屈服应力的 2/3。当仅存在膜应力时,抵抗塑性破坏安全系数为 1.5。
- 膜应力与弯曲应力之和的应力强度不应超过屈服应力。如果仅存在弯曲应力,则抗破坏的安全系数也为 1.5。这是因为在这种情况下,初始屈服不等于截面的完全屈服破坏。
- 有类似的需求,但需要具有更高的安全系数,以防止达到极限应力。
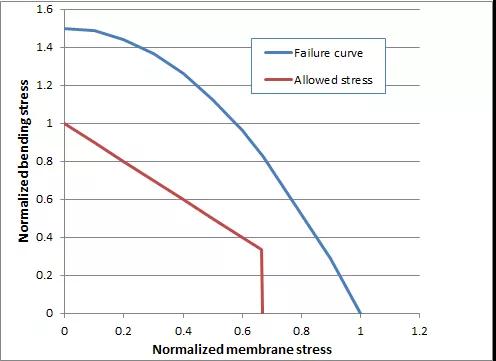
有趣的是,如果膜应力正好达到第一个标准所允许的极限值,仍允许增加一定量的弯曲应力。由上文的讨论可知,这是因为弯曲应力减少了部分截面应力。如上所述,当涉及静态失效时,具体的应力状态并不重要,因为破坏状态下的应力分布完全由力和力矩平衡确定。在下图中,将破坏作用曲线与规范规定的应力极限进行了比较。应当指出,由于高压容器通常在高温下运行,因此允许应力的室温值可能不够充足。为了避免在每个载荷循环中积累塑性应变,因低周疲劳而导致快速失效,要求次应力避免重复加载-卸载循环时的循环塑性变形。