铝合金尖端试验的有限元模拟
铝合金尖端试验的有限元模拟
有限元模拟在提高大块金属成形过程设计的效率和有效性方面得到了广泛的应用。在模拟中, 合理考虑摩擦条件是获得可靠结果的重要条件,为此,剪切摩擦系数被广泛应用于体变形模拟中。在早期估计剪 切摩擦系数的工作中,在工件的后挤压端形成了一个名为“尖端试验”的径向尖端。结果表明,通过简单地测量变形AL6061-0工件的径向端部距离,可以有效地确定剪切摩擦系数,因为两者是线性关系。在本研究中, 基于有限元模拟确定了凹模与底模界面的摩擦条件。底模的剪切摩擦 系数约为冲头剪切摩擦系数的60%。预测的剪 切摩擦系数与环压试验得到的值比较良好。
关键词:提示测试,径向距离提示,反向挤压,剪切摩擦系数,有限元模拟
随着最近对净形状成形的需求的增加,需要更有效的设计已成为一个重要的问题。因此, 为了减少开发时间和成本,在金属成形操作的设计中使用计算机已变得广泛,而不是使用基于实验、经验和反复试验的传统设计方法。基于有 限元法的金属成形过程数值分析已成为产品开发过程和模具设计阶段的常用工具。为了 使这种有限元模拟可靠,准确地描述摩擦条件是至关重要的。材料流动与摩擦条件直接相关,摩擦条件影响着成型所需的载荷和最终产品的力学性能。产品质 量的其他方面,如表面光洁度和尺寸精度也是受摩擦条件的影响。此外, 刀具设计、刀具寿命和生产率取决于确定和控制摩擦的能力。
迄今为止,常剪切摩擦模型是最广泛地用于定量描述大块金属成形过程中的摩擦条件。为使恒剪切摩擦模型得到有效应用,必须根据润滑条件确定适当的剪切摩擦系数。
为了评价大块金属成形过程中的摩擦状态,人们提出了多种测试方法。例如, 环压试验[1-3]因试验简单而得到广泛应用。然而, 由于其简单性,从环压试验中得到的剪切摩擦系数可能并不总是适用于实际的金属成形过程。
因此,提出了基于其它成形过程的摩擦试验方法。然而,这些方法如钉锻试验[4,5]、桶形试验[6]、注入式上置[7]、前后挤压组合[8-12],大多需要非线性校准曲线,试验装备在设计和操作上都比较复杂。Naka- mura等人[13]提出了一种基于后向挤压的叶尖试验,但这种方法对成形载荷的依赖性太大。
最近,Im等人[14]提出了基于后向挤压的叶尖试验,通过测量叶尖到变形工件侧壁的径向距离来确定摩擦条件。在本工作中, 实验测试表明,将初始工件直径设置为冲头外径与下模腔内径之间的值,径向尖端形成于工件挤压端。通过对各种润滑剂的试验发现,摩擦量越大,摩擦尖端到试样外表面的径向距离越大,最大成形载荷越大。通过绘制各润滑剂的叶尖径向距离和最大成形载荷,发现两者之间呈线性关系。这表明,径向叶尖距离的简单几何测量可以有效地作为摩擦条件的指示器。
本研究是将测量的叶尖径向距离与剪切摩擦系数直接联系起来的后续研究。在各种剪切摩擦因子下,对提出的后挤压过程进行了大量的有限元分析。如所料,由于叶尖径向距离与最大成形载荷呈线性关系,可以认为叶尖径向距离与剪切摩擦系数也呈线性关系。然而,在反挤压过程中,冲头和下模界面的摩擦条件可能并不总是相同的。事实上,在[12]反挤压过程的数值模拟中,通常会给冲头指定较高的剪切摩擦系数,而不是模具。
因此,在模具处的剪切摩擦系数数值上由凹模所赋值的一定百分比来确定,以便使由模拟和实验得到的最大成形载荷与叶尖径向距离曲线的斜率平行。用数值方法确定 了不同润滑油的剪切摩擦系数、径向叶尖距离和形态载荷之间的线性关系。并将线性关系预测的剪切摩擦系数与环压试验结果进行了比较。
2、数值模拟
在目前的研究中,用于有限元模拟的冲模和模具的尺寸与实验中使用的模具尺寸[14]一致。模拟条件与实验设置尽可能接近。对于nu- merical分析,使用了用于金属成形分析的内部FE程序CAMPform2D[15-18]。
在当前的模组中,最初的圆柱形工件被制造为直径为30毫米,高度为15毫米。然后, 该工件通过放置在较低的模具中心。

图1. 定心槽对料流的影响:(a)工件初始绘底面,(b)行程4.8 mm时工件底部
它在一个浅槽深度0.3毫米。由于沟槽深度不是很大, 本文研究了在有限元模拟中是否可以忽略沟槽。首先在变形前对工件的底部进行喷漆,检查在反挤压过程中,工件的底部表面是否在凹槽上移动或恢复到原来的位置。
如图1所示,变形过程中,被涂漆的底面仍在凹槽内。这说明,为了准确地模拟当前工艺,必须考虑沟槽。同时,测量了实验得到的4.8 mm行程下工件的变形形态,并与考虑和不考虑浅槽情况下的有限元模拟结果进行了比较。对比如图2所示。结果表明,在当前的有限元模拟中可以适当地考虑沟槽的存在。
在不同剪切摩擦因子下进行了有限元模拟,研究了剪切摩擦因子对成形过程中刀尖距离和成形载荷的影响。通过以润滑脂为润滑剂的相同尺寸的针尖试验试件的压缩试验,得到AL6061-O的流动应力为 σ¯ 241.9ε¯0.39MPa,其中σ¯ 和 ε¯分别为有效应力,为有效应变。
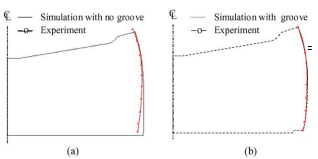
图2. (a)无定心槽和(b)行程4.8mm时考虑定心槽的试验和模拟试验的变形形状比较

图3. 有限元模拟实例(a)条件和(b)结果显示了变形形态和有效应变分布
在这个例子中,假设剪切摩擦系数处处为0.1。图3(a)为一个被调查的典型案例。详细信息的模切试可在参考资料[14]找到。冲头速度设定为5.0mm/s,停止冲头行程设定为8mm。为适应下模的浅槽而制作的初始工件由1156个等参节点和1089个四边形单元初步建模。由于轴对称问题,仅使用了工件尺寸的一半(15mm 15mm)。为了在模拟过程中仔细考虑浅槽的影响,需要大约43个雷梅斯元来完成数值计算。
仿真实例结果如图3(b)所示。这里显示了挤压后工件的变形形状以及有效应变的分布。可以确定,目前的反挤压设置导致挤压端产生径向尖端,径向尖端与试样外侧面有一定距离d。在模拟结果中也可以看到槽区中大量的精细元素用于提高模拟精度。
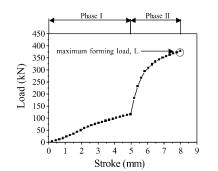
图4. 通过有限元模拟得到剪切摩擦系数为0.1时的载荷与行程曲线
图4为仿真算例的成形载荷随行程的变化情况。从这条曲线可以看出,成形载荷在镦粗阶段稳定增加,在工件开始向后挤压时急剧增加,最后挤压时趋于平稳。最大成形载荷L为图中在8mm行程时计算的载荷。
在0-0.9范围内,以0.1为增量,进行了10次模拟,研究了其对径向叶尖距离和最大成形载荷形成的影响。与实验结果相似,仿真结果表明,最大成形载荷L与叶尖径向距离d呈线性关系。 L/L0.9被绘制为线性函数的d/t,如图5所示,在L0.9(644 kN)是最小形成负载模拟使用剪切摩擦系数为0.9时和t(3.4毫米)被挤压变形的工件的厚度。
从图中可以看出,L/L0.9与d/t图的斜率在模拟结果和实验结果中是不同的。同时还发现,实验得到的叶尖径向距离的测量值并不都在模拟得到的叶尖径向距离范围内。例如,使用0.9剪切摩擦系数模拟得到的d/t最大值仅为0.4,而使用润滑脂试验得到的实际测量值。
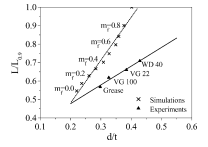
Fig. 5 在剪切摩擦系数为0.0 ~ 0.9的情况下进行有限元模拟,并使用各种润滑剂进行试验,得到载荷与叶尖径向距离的关系曲线
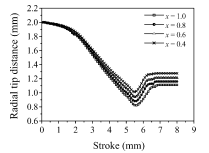
Fig. 6 当mfp固定为0.5时,径向叶尖距离随x变化的关系
WD40为0.43。实验结果与模拟结果之间的这种差异表明,对冲模和冲模采用相同的剪切摩擦系数的模拟条件可能不合适。
因此,进行了数值试验,使模具的剪切摩擦系数,mfd, 由于只给了冲头一定的百分比,mfp。那是mfd/mfp=x,在这里0.0x 1.0. 为了使模拟和实验得到的最大成形载荷与叶尖径向距离曲线的斜率平行,引入了该方法。
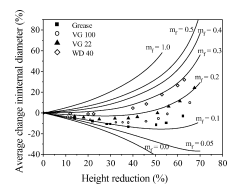
为了研究x对成形载荷的影响,进行了有限元数值模拟。假设mfp为0.5时,x在1.0、0.8、0.6和0.4之间变化。这导致径向叶尖距离1.113, 1.160, 1.213, 1.276毫米。此外,最终成形载荷分别为482、462、448和431 kN。图6显示了径向的变化提示从一面墙提示测试期间,根据x。可以看出,径向提示首先走向面墙在镦粗和初始反向挤压阶段,以及反向挤压所得径向提示移动相反的direc,穿孔。一旦径向端部通过冲孔地区,端部的径向部分不改变。总体上可以看出,终径向叶尖距离随着x值的减小而增大。图7给出了四种模拟工况的载荷与行程曲线,从图中可以看出,镦粗阶段的成形载荷差异不大,但在反挤压阶段,随着x值的增大,成形载荷增大。这些结果表明,计算得到的斜率L/L0.9相对于d/t图可以平行于 L/L0.9相对于由实验得到的图形,取决于x的值。
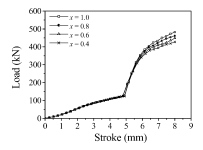
Fig. 7 当mfp固定为0.5时,成形载荷对x的依赖性变化
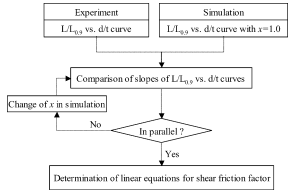
Fig. 8 获得预测剪切摩擦系数的线性方程的过程
3、剪切摩擦系数的估算
从上面的发现,很明显,为了使模拟与实验更一致,必须首先找到x。同时比较了有限元模拟和实验结果得到的径向叶尖距离和成形载荷。图8显示了这一总体过程,从而得到了预测剪切摩擦系数的线性方程。
如前所述,通过绘制无量纲化的最大载荷,得到如图5所示的载荷与叶尖径向分布曲线。 L/L0.9, 和径向叶尖距离,d/t为各种剪切摩擦因子。更具体地说,冲裁模的剪切摩擦系数在0.1 ~ 0.9之间变化。
为了确定x对载荷随叶尖径向距离曲线的影响,除了将x从1.0改为0.8、0.6和0.4外,还进行了类似的模拟。图9给出了这些模拟的结果,可以清楚地看出,曲线的斜率随着x的变化而变化。同时可以看出,无论x的取值如何,径向叶尖距离与最大成形载荷之间的线性关系保持不变。
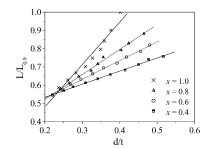
Fig. 9 在mfp的各种摩擦条件下,载荷与叶尖径向距离的关系曲线取决于x的值,范围从0.0到0.9

Fig. 10 在x = 0.6时,计算器与仿真器之间的负荷与叶尖径向距离图的比较.
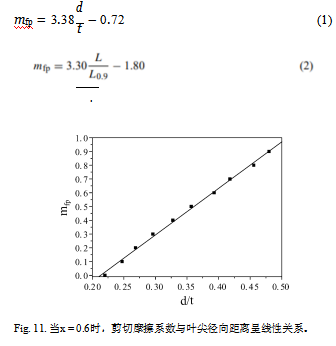
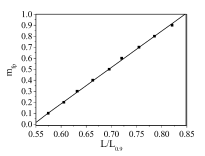
Fig. 12 当x = 0.6时,剪切摩擦系数与最大成形载荷呈线性关系。
如图10所示,在x = 0.6的模拟情况下,得到的斜率与实验情况最吻合。从这一结果可以看出,在反挤压过程中,冲头界面处的摩擦水平要高于模具界面处的摩擦水平。虽然从实验和模拟中得到的图的斜率是平行的,但是在这个图中两者之间存在一个小的差距。实验结果与仿真结果的总负载误差约为8.5%。这种错误可能是由于材料特性,以及与测量尖端距离和成形负荷有关的机器和人为错误。
由于每个无量纲的最大成形载荷,L/L0.9,在负载和径向提示距离曲线对应荷兰国际集团(ing)全球平均剪切摩擦值,负载和径向提示距离曲线的结果使用x=0.6条件下可以直接转化为剪切摩擦系数和径向距离和剪切摩擦系数和负荷曲线根据这两个之间的线性如无花果。11和12所示。
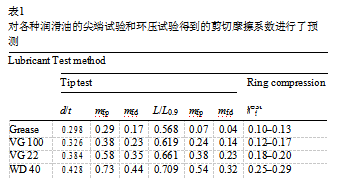
这些线性表达式现在可以用来预测不同润滑条件下冲模和冲模之间的固有剪切摩擦因子。通过将无量纲径向叶尖距离和从膨胀件测量的最大成形载荷插入到方程式中。(1)和(2),可以很容易地计算出相应的冲模与模具之间的剪切摩擦系数。按不同润滑方式计算的剪切摩擦系数如表1所示。
如表1所示,在润滑VG 100的情况下,虽然通过实验和仿真得到的径向叶尖距离,但Eq.(1)预测的全球平均剪切摩擦因子要高于Eq.(2)预测的mfp=0.38和mfd=0.23 是否与模拟得到的0.384,行程8mm时的载荷429kN相同。
大于实验得到的395kN,如图13所示。实验结果与仿真结果的总负载误差约为8.5%。另一方面,采用mfp=0.24和mfd=0.14的实验和模拟得到的载荷与0.619相同,但实验得到的1.108mm径向叶尖距离高于模拟得到的0.967 mm径向叶尖距离。本例的径向叶尖距离误差约为13%。
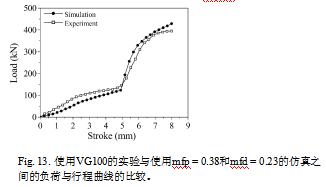
Fig. 13 使用VG100的实验与使用mfp = 0.38和mfd = 0.23的仿真之间的负荷与行程曲线的比较
然而,如果一个线性校准曲线拟合这两个模拟和实验图在图10中使用,可以减少这些错误进一步,然后两个剪切摩擦因素根据径向距离和成形载荷剪切摩擦系数可以表示为一个代表补偿这些错误。同时,在不考虑实际中随位置和时间变化的实际摩擦条件的情况下,采用剪切摩擦模型时,不可避免地会出现实验结果与仿真结果之间的误差。
该方法预测了各润滑油的全球平均剪切摩擦因子mfp和mfd。这些数值与相同润滑油的环压试验结果进行了比较。通过环压试验得到的实验结果及校准曲线如图14所示。由环压试验确定的剪切摩擦系数也总结在表1中。这个表中可以看到,预测剪切摩擦系数提示测试大约是在穿孔的两到三倍的价值,通过环为每个润滑剂进行压缩试验,而类似于一个,死于压缩试验。可以认为复杂成形过程的整体剪切摩擦系数为mfd和mfp之间的值,取决于变形时新表面产生的程度。
在本研究中,为确定铝合金反挤压过程的摩擦条件,进行了一套尖端试验。实验观察到,随着摩擦量的增加,试样从叶尖到侧壁的径向距离增大,可以作为衡量摩擦条件的有效手段。当mfd/mfp=0.6时,径向端部位置对冲头处摩擦条件的变化比模具处更敏感,冲头界面处的整体平均摩擦水平高于模具界面处的平均摩擦水平。有限元模拟结果也清楚地证实了叶尖径向距离、成形载荷和剪切摩擦系数之间的关系是线性的。这说明了通过测量叶尖摩擦系数或成形载荷来确定整体平均剪切摩擦系数的方法是可行的。由于所提出的方法既包括镦粗变形,也包括反挤压变形,因此可以很好地描述实际块体成形过程中的摩擦条件。
转载请注明精川材料检测地址:www.jctest.vip




