有关有限元分析的那些基本认识
在有限元分析领域,大家似乎看到过很多缩写,比如CAE、FEM、FE、CFD、FEA等等,但从英文全程来看其实他们区别不大。比如CAE,英文全称是Computer Aided Engineering,即计算机辅助工程;FEM,Finite Element Method,即有限元方法;FEA,Finite Element Analysis,有限元分析;CFD,Computational Fluid Dynamics,计算机流体动力学。可以看出,除了CFD强调流体以外,FEA、CAE、FEM其实都是一个范畴的,即有限元法相关,其实CFD也是他们的一个分支。为了统一,我们取FEA为有限元分析的简称。
什么是FEA呢?我们来简单介绍一下。
在数学上,有限元方法(Finite Element Method)是一种为偏微分方程的边界值问题寻找近似解的数值计算方法,既然是数值计算方法,所以是没有精确解的。它将一个区域分成简单的小单元,这些小单元称为有限元,并使用各种微积分的各种求解方法在最小误差函数下求解问题。类似于连接许多小段直线可以近似逼近一个圆一样,有限元法综合每个小单元的方程去近似逼近整个大范围内的方程域。
离散化实例:

这个比喻我想大家都容易理解,通过无限个三角形去逼近一个圆形,由数学的极限可知,只要三角形最够多,误差就会趋向于0。而实际模型就是通过很多微小的实体或平面单元去逼近的,那么实际模型可以用无限个单元去逼近吗,显然是不可能的(单元划分大小的选择会在后续详细讲解)。离散化以后,单元间是通过节点相连接点,这个连接节点是非常重要的,因为:
在计算机求解时,每个节点都是输入/输出源
加载力会在相互连接的节点间传递
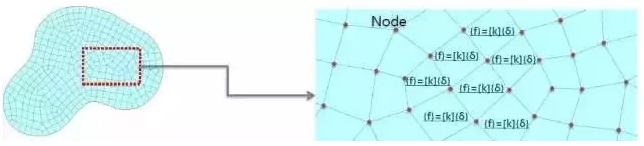
如下图,每个单元都由相应的控制方程所诠释,而节点是沟通这些方程的媒介,有了节点,就能构造庞大的模型
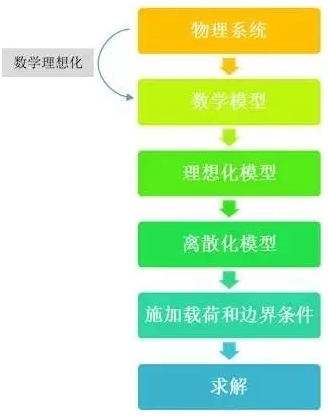
下面说说一般的FEA分析流程如下:
举个例子:
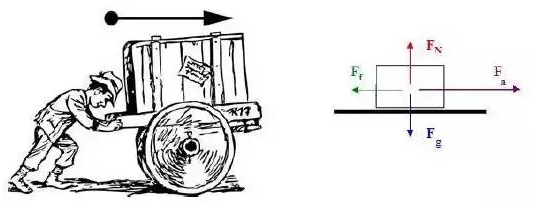
有限元分析的对象是现实世界中的物理模型,当我们面对一个实际的对象时,我们首先要做的是构建数学模型,比如上面推车的例子,我们要先分析出模型的受力,从物理系统到数学模型的理想化是第一步,我们要做到:
理解物理系统的力学形式
使用理论物理的方法建立数学关系
理解数学模型背后的隐含假设
获得分析所需的边界条件(如约束和加载力)
这里我们最需要的就是边界条件,有了边界条件我们才能在后续施加正确的条件来求解。
有了模型,那么我们就该离散化了,也就是划分网格了,那么我们就直接划分网格吗,这是初学者容易犯的错误,拿到一个模型就开始划分网格,而且我猜几乎都是3D四面体网格。
我得告诉大家,有限元分析最费时的部分就是划分网格,网格划分好了,后面求解就是分分钟的事情,大不了就是等计算机算完。为了获得可靠的结果又节约求解时间,复杂的模型划分甚至能耗去几小时,几天或者几周的时间。
一般来说,3D六面体网格会比3D四面体来得精确,3D四面体网格是非结构化网格(和节点相连的网格类型不相同,比如一个四面体和六面体共用了同一个节点),3D六面体网格是结构化网格(和节点相连的网格类型相同)。
非结构化网格最大的特点是能划分任意复杂的模型,而且时间快,但网格比结构化网格多几倍,求解时间会很慢,而且结果的收敛性没有结构化网格好。如下图:
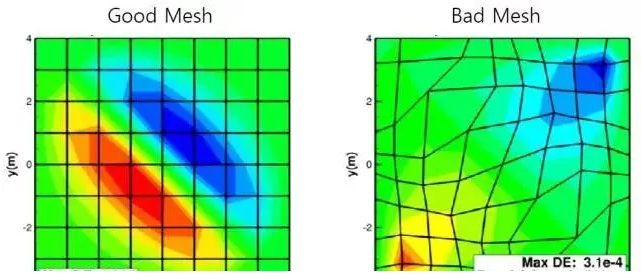
如果网格划分不好,结果会大相径庭。所以面对一个模型我们要综合考虑各种因素来选择划分的网格类型,况且除了3D单元以外,还有1D和2D单元,不同的场合选择也是不一样的。
其实大多数情况下我们会采用3D四面体网格,但不是所有样子的3D四面体网格都是可行的,我们需要检查其各种参数,比如长宽比,扭曲系数,雅可比因子等等,只有通过一定的参数检查,我们才能保证结果的准确。
另外在划分网格以前,我们还要对模型进行处理,也称为模型理想化,既要把对分析结果没什么影响的结构给去掉,比如细小孔和其它细微结构,还有就是有问题的地方比如破面等要修复。
为什么这样做呢,在FEA分析领域有这样一句话:The detail of model is a dream of CAD designer,but a nightmare of CAEer(模型的细节是CAD设计人员的梦想,却是CAE仿真人员的恶梦)。
可见,如果一个结构太过于细微,那么网格划分是很难成功的,所以我们要先理想化地去除,因为这些细节对结果是没有多大影响的。
网格划分的好,边界条件也有了,那么后面的求解和后处理也就变得很简单了。
转载请注明精川材料检测地址:www.jctest.vip




